二元关系

序偶：两个元素 $x,y$ 按照一定次序组成的二元组称为有序偶对 记作 $<x,y>$ ,其中x是第一元素,y是第二元素
1
笛卡尔积: 设 $A,B$ 是两个集合,称集合

NOTE

$A\times B=\{|<x,y>|x\in A\cap y\in B\}$
为集合A与B的笛卡尔积(Cartesian Product)

[!summary] 笛卡尔积的计算

1. AB笛卡尔积是以序偶为元素的集合
2. 序偶的第一元素遍历A中的元素,第二元素遍历B中的元素
3. 当A,B都是有限集时, $|A\times B|=|B\times A|=|A|\times |B|$ .
4. 两个集合的笛卡尔积不满足交换律
5. $A\times B=\mathrm{\varnothing }\iff A=\mathrm{\varnothing }\vee B=\mathrm{\varnothing }$

例如: $A=\{1,2,3\},B=\{a,b,c\}?$
$A\times B=\{<1,a>,<1,b>,<1,c>,<2,a>,<2,b>,\dots \}$
$B\times A=\{<a,1>,<a,2>,<a,3>,<b,1>,\dots \}$
显然 $A\times B\ne B\times AthenCartesianProduct$

定理 1. 设A,B,C是任意3个集合,则

1. $A\times (B\cup C)=(A\times B)\cup (A\times C)$
2. $(B\cup C)\times A=(B\times A)\cup (C\times A)$
3. $A\times (B\cap C)=A\times B\cap A\times C$
4. 和上面一样

定理 2. 设A,B,C,D是任意四个非空集合,则 $A\times B\in C\times D\iff A\in C,B\in D$

关系的定义

关系中R为子集
定义5 设AB为两个非空集合,称 $A\times B$ 的任意子集 $R$ 为从 A到B的一个二元关系,简称关系. 记作 $R:A\to B$.
如果 A = B ,则称R为A上的一个二元关系,记作 $R:A\to A$
序偶 $<x,y>\in R\mathrm{可}\mathrm{记}\mathrm{作}xRy$
全关系: $R=A\times B$
空关系: $R=\mathrm{\varnothing }$
恒等关系: $R=I_A=\{<x,x>|x\in A\}$ 例如 $A=\{1,2\},I_A=\{<1,1>,<2,2>\}$
空集是任何集合上的关系
例4 假设 $A=\{1,2\},\mathrm{判}\mathrm{断}\mathrm{下}\mathrm{列}\mathrm{集}\mathrm{合}\mathrm{是}\mathrm{否}\mathrm{是}A\mathrm{上}\mathrm{的}\mathrm{关}\mathrm{系}:$
$A\mathrm{上}\mathrm{的}\mathrm{关}\mathrm{系}=A\times A=\{<1,1>,<1,2>,<2,1>,<2,2>\}$

1. $T_1=\mathrm{\varnothing }$ 是的
2. $T_2=A\times A$ 显然 $A\mathrm{上}\mathrm{的}\mathrm{关}\mathrm{系}=A\times A$
3. $T_3=\{<1,1>,<2,2>\}$ 显然
4. $T_4=\{<1,1>,<2,1>\}$ 显然
5. $T_5=\{<1,1>,<2,2>,<2,1>,<<1,1>,1>\}$ 前三个是 第三个不是

定义6 $\mathrm{设}{A}_1,A_2,\dots ,A_n\mathrm{为}n\mathrm{个}\mathrm{非}\mathrm{空}\mathrm{集}\mathrm{合},\mathrm{则}\mathrm{称}{A}_1\times A_2\times \cdots \times A_n\mathrm{为}\mathrm{以}{A}_1\times A_2\times \cdots \times A_n\mathrm{为}\mathbf{\text{基}}\mathrm{的}n\mathrm{元}\mathrm{关}\mathrm{系}(n-aryRelation)$

关系的表示法

列举法

关系图 即邻接表

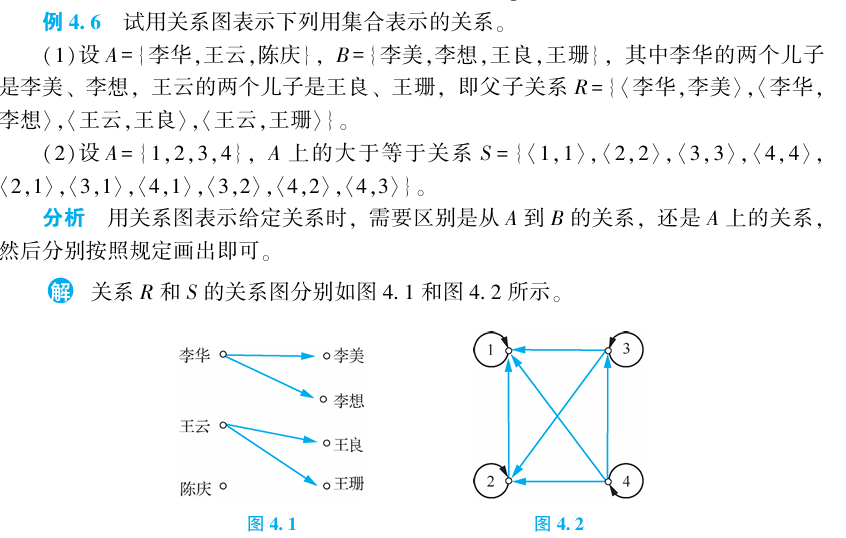
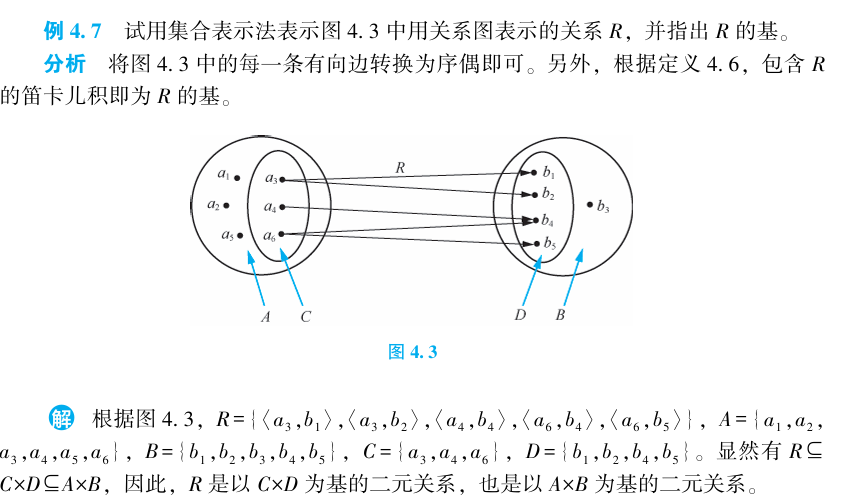
*前域后域*

在一个关系中,若构成关系的两个集合C,D分别是另两个集合A,B的子集,则 称A是R的前域,B是R的后域,C是R的定义域(Domain) 记作 $C=domR$ ,D是R的值域(Range)记作$D=ranR$, $fldR=domR\cup ranR$ 称为 R的域(Field)

关系矩阵 即邻接矩阵

关系矩阵也是[[布尔矩阵]]

布尔并

定义7 若$A,B$ 皆为 $m\times n$ 的矩阵,则 A和B的布尔并也是 $m\times n$矩阵, 记作 $A\vee B$ 有 1 则 1 无1 则0

布尔交

条件与上面相同,记作 $A\wedge B$ 有0则0 无0则1

布尔积

和矩阵乘法相同

关系的运算

与集合基本相同
根据补运算的定义 由于 $A\times B\mathrm{是}\mathrm{相}\mathrm{对}\mathrm{于}R\mathrm{的}\mathrm{全}\mathrm{集},\mathrm{所}\mathrm{以}\mathrm{有}$

1. $R^c=A\times B-R$
2. $R^c\cup R=A\times B$
3. $R^c\cap R=\mathrm{\varnothing }$
4. $(R^c{)}^c=R$
5. $S\subseteq R\iff R^c\subseteq S^c$
   

复合运算

定义 8 $\mathrm{设}\mathrm{有}A,B,C\mathrm{三}\mathrm{个}\mathrm{集}\mathrm{合},R:A\to B,S:B\to C$,则R与S的复合关系(合成关系)(Composite Relation) 是 A到C的关系,记为 $R\circ S$ ,其中 $R\circ S=\{<x,z>|x\in A\wedge z\in C\wedge \mathrm{\exists }y(y\in B\wedge <x,y>\in R\wedge <y,z>\in S)\}$
人话 取所有 y 作为中间关系 跳到 <x,z>

定理4.4 符合关系满足

1. 结合律$(R\circ S)\circ T=R\circ (S\circ T)$
2. $I_A\circ R=R\circ I_B=R$
   
   不满足交换律

逆运算

交换序偶位置
$R^{-1}=\{<b,a>|<a,b>\in R\}$
$(A\times B{)}^{-1}=B\times A$
转置运算
$|R|=|R^{-}1|$
$(R\circ S{)}^{-1}=S^{-1}\circ R^{-1}$

幂运算

$\mathrm{设}R：A\to A，\mathrm{则}R\mathrm{的}n\mathrm{次}\mathrm{幂}\mathrm{记}\mathrm{为}{R}^n,\mathrm{定}\mathrm{义}\mathrm{如}\mathrm{下}$:

1. $R^0=I_A$
2. $R^1=R$
3. $R^{(n+1)}=R^n\circ R=R\circ R^n$
4. $R^n\mathrm{任}\mathrm{然}\mathrm{是}A\mathrm{上}\mathrm{的}\mathrm{关}\mathrm{系},\mathrm{并}\mathrm{且}{R}^n\circ R^m=R^{n+m},(R^m{)}^n=R^{mn}$
5. 定理4.8$\bigcup _{i=1}^{\mathrm{\infty }}{R}^i=\bigcup _{i=1}^n{R}^i\mathrm{其}\mathrm{中}n=|A|$

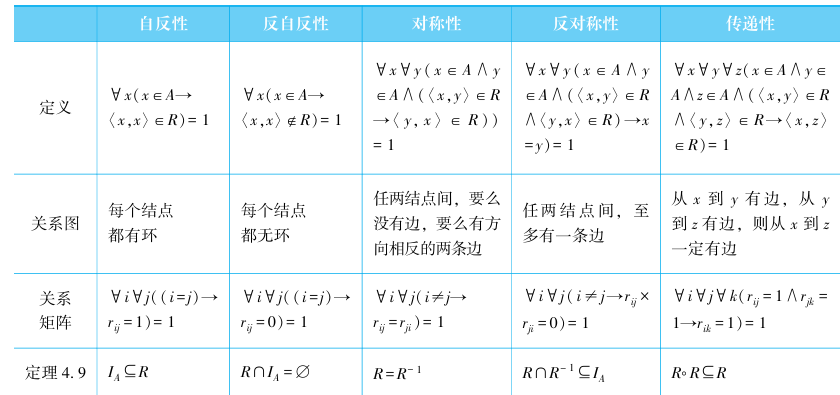
关系的性质